АЛГОРИТМ ЗАЛИВКИ ЗАМКНУТОГО КОНТУРА
Р. П. Худеев
При решении одной из прикладных задач возникла необходимость заливки замкнутого контура. Поиск дал несколько вариантов решения этой задачи [1-4], но эти варианты нам не подошли из-за большого количества вычислений на контурах, содержащих большое количество точек внутри контура, и, как результат, из-за низкой скорости работы. Кроме того, существующие алгоритмы не позволяют заливать сложные контуры, содержащие самопересечения.
Предложенный вариант характеризуется простой логикой работы, простотой реализации и высокой скоростью работы. В данном методе не используются тригонометрические функции, операции деления и умножения, а так же рекурсивные алгоритмы. В отличие от рекурсивных алгоритмов, в которых количество проверок доходит до 4 или 8 (в зависимости от алгоритма и типа контура) на каждую точку внутри контура, в нашем алгоритме количество проверок в среднем не превышает 2 на каждую точку контура. Это значительно ускоряет процесс заливки на контурах, в которых количество точек внутри контура значительно больше количества точек контура. Кроме того, данный метод позволяет заливать самопересекающиеся контура - как целиком, так и любые его части по отдельности.
Итак, задача:
Дан массив точек, размером X на Y.
Имеем замкнутый четырех- или восьми- связный контур, точки которого по цвету отличаются от фоновых точек (рис.1).
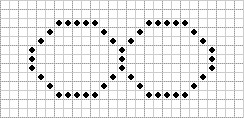
Рис.1
Необходимо залить все области, находящиеся внутри, либо снаружи данного контура.
Описание алгоритма:
Суть алгоритма заключается в том, чтобы поверх существующего "внутреннего контура" построить "внешний контур", а затем построчно заливать области, в которых между двумя соседними точками "внешнего контура" есть хотя бы одна точка "внутреннего контура". Для этого необходимо выполнить следующие шаги:
1. Необходимо найти любую "наружную" точку контура. Эта точка может быть задана, либо для ее нахождения нужно построчно сканировать изображение до попадания на любую точку контура (рис. 2).
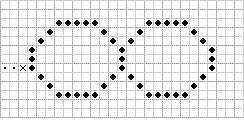
Рис.2
2. Строим "внешний контур". Для этого от точки, которую мы нашли в пункте 1, последовательно, в любом направлении, обходим контур и отмечаем точки внешнего контура (рис. 3).
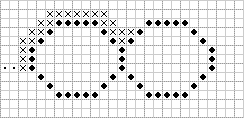
Рис.3
Алгоритм построения "внешнего контура" может быть следующий - у нас имеется первая точка "внешнего контура" (обозначена буквой А на рис. 4), найденная в результате построчного сканирования. Для этой и последующих точек нужно определить первое попавшееся "свободное" направление, переместится на одну точку в этом направлении и пометить эту точку как следующую точку "внешнего контура". Далее процесс повторяется до полного построения "внешнего контура". "Свободным" направлением считается одно из четырех возможных направлений, при переходе по которому мы не попадаем на точку "внутреннего контура". Направление, при переходе по которому на следующую точку мы попадаем на точку "внешнего контура", тоже считается "свободным". При этом проверка четырех возможных направлений должна осуществляться всегда только по часовой, либо против часовой стрелки. В нашем примере проверка осуществляется против часовой стрелки. Последовательность проверки направлений точек A-G "внешнего контура" на рисунке обозначена цифрами. Сначала проверяется направление под номером 1, затем 2, 3 и 4. Правило выбора направления 1 следующее - для первой точки направление 1 совпадает с ближайшей точкой "внутреннего контура", для всех остальных точек направление 1 определятся как следующее против часовой стрелки направление от того, с которого мы пришли с предыдущей точки, т.е. направление, откуда мы пришли всегда будет по номером 4. Для наглядности на рис. 4, показана последовательность проверки направлений для нескольких точек "внешнего контура". Вышеописанное правила позволяют построить "внешний контур" с максимальной скоростью, то есть с минимальным количеством проверок "свободных" направлений.
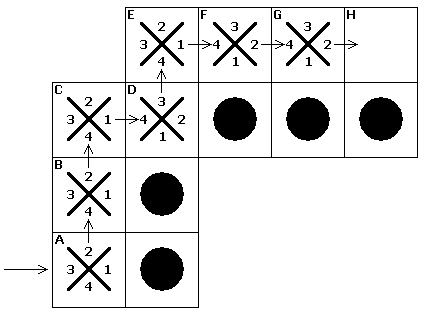
Рис.4
Процесс построения "внешнего контура" заканчивается, когда координаты текущей точки совпадут с координатами начальной точки "внешнего контура" (рис. 5).
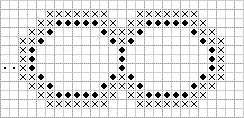
Рис.5
3. Теперь нужно построчно просканировать прямоугольник, в который вписан контур и при обнаружении между двумя соседними точками "внешнего" контура хотя бы одной точки "внутреннего" контура мы должны залить всю часть стрики между точками "внешнего" контура, и, при необходимости (если заливка не совпадает с цветом контура), можно исключить из заливки точки "внутреннего" контура. (рис. 6, 7).
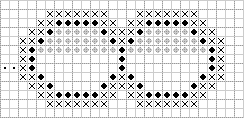
Рис.6
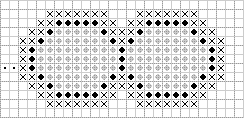
Рис.7
По такому же принципу можно залить все точки вне контура, для этого после построения "внешнего контура", нужно построчно сканировать картинку и если между границей изображения и точкой "внешнего контура" нет точек "внутреннего контура", либо между двумя точками "внешнего контура" нет точек "внутреннего контура", все точки можно закрашивать цветом заливки.
Если необходимо залить область внутри контура, это можно сделать по такому же принципу. Только в этом случае существующий контур нужно считать "внешним". Далее строится "внутренний контур", и, если между двумя точками "внутреннего контура" нет точек "внешнего контура", все точки между точками "внутреннего контура" можно закрашивать цветом заливки.
Таким образом предложенный алгоритм, в отличии от существующих, позволяет залить все внутренние области как простого, так и самопересекающегося контура любой конфигурации. Также можно залить любую из внутренних областей самопересекающегося контура. Кроме того, данный алгоритм эффективней по скорости работы на тех контурах, количество точек внутри которых значительно больше количества точек самого контура.
Литература
[1] Роджерс Д. Алгоритмические основы машинной графики. Пер. с англ. М.: Мир, 1989. 512 c.
[2] П.В.Вельтмандер МАШИННАЯ ГРАФИКА (Учебное пособие в 3-х книгах) Книга 2. Новосибирский государственный университет, 1997 ISBN5-230-13606-5
[3] http://alglib.sources.ru/graphics/fillarea.php
[4] http://algolist.manual.ru/graphics/fill.php